The potential above the plane is easily found by placing an image charge below the plane.
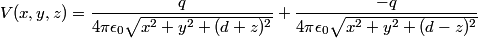 The induced charge density on the conducting plane can be found using Gauss's Law 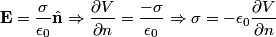 Therefore, 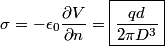 Therefore, answer (D) is correct. |
The potential above the plane is easily found by placing an image charge below the plane.
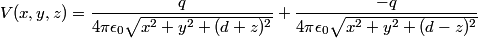 The induced charge density on the conducting plane can be found using Gauss's Law 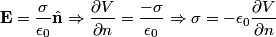 Therefore, 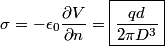 Therefore, answer (D) is correct. |